The Road Ahead week2 Boolean Arithmetic and the ALU

Posted on | In ,

“The great wall is made by blocks”

二进制加法

半加器

我们考虑最基本的二进制加法，两位相加，然后再扩展到高位上。对于一个对a, b两位相加的加法器，我们称其为半加器，输入是a, b两位，输出为和sum以及进位carry

图片名称

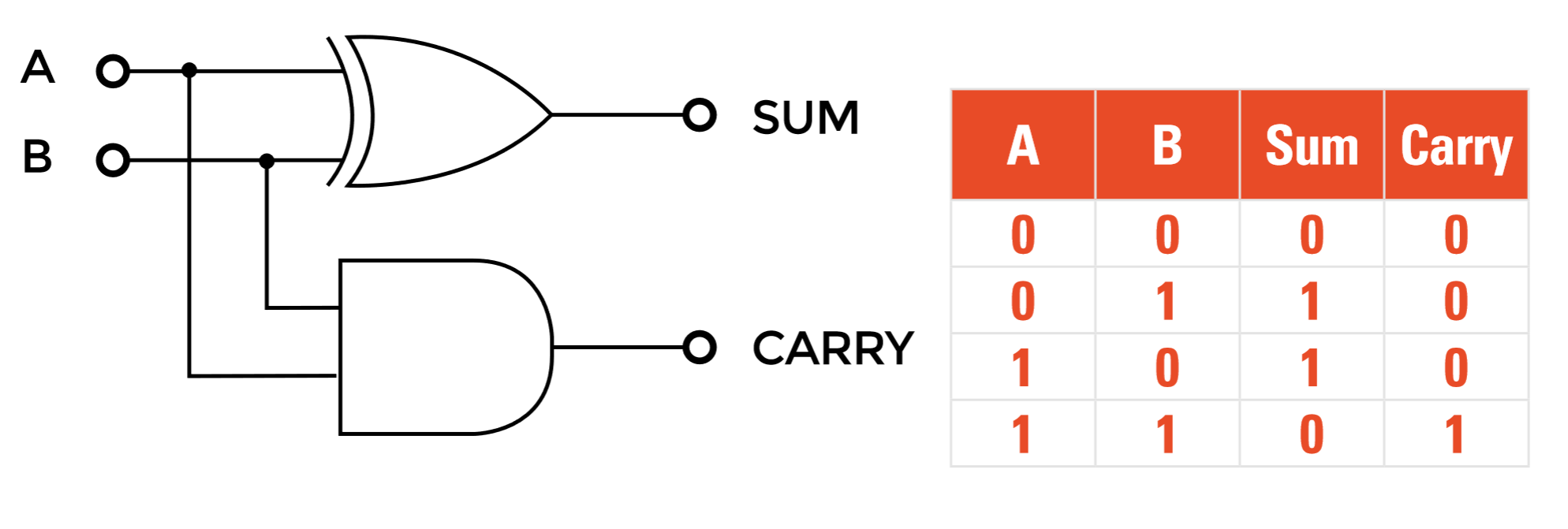
半加器实际上就是不考虑输入进位的加法器

全加器

现在我们考虑进位，引入全加器，即在输入端考虑有进位的情况，全加器的真值表如下：

c b a sum(out) carry(out)
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1

实际上全加器就是计算( a + b + carry)，可以用两个半加器实现，实现方式如下：

图片名称

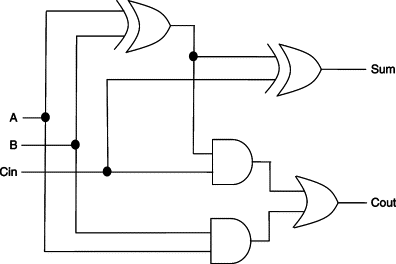
多位加法器

现在我们来考虑如何实现多位加法，一样的道理，对于每一位运算，我们可以使用一个全加器，对于第一位，输入的carry设置为0即可，也不难，这里来直接给出HDL实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// This file is part of www.nand2tetris.org
// and the book "The Elements of Computing Systems"
// by Nisan and Schocken, MIT Press.
// File name: projects/02/Adder16.hdl

/**
 * Adds two 16-bit values.
 * The most significant carry bit is ignored.
 */

CHIP Add16 {
    IN a[16], b[16];
    OUT out[16];

    PARTS:
    // Put you code here:
    HalfAdder(a = a[0], b = b[0],            sum = out[0],  carry = c0);    // The first bit not have a carry, use a half adder
    FullAdder(a = a[1], b = b[1],   c = c0,  sum = out[1],  carry = c1);
    FullAdder(a = a[2], b = b[2],   c = c1,  sum = out[2],  carry = c2);
    FullAdder(a = a[3], b = b[3],   c = c2,  sum = out[3],  carry = c3);

    FullAdder(a = a[4], b = b[4],   c = c3,  sum = out[4],  carry = c4);
    FullAdder(a = a[5], b = b[5],   c = c4,  sum = out[5],  carry = c5);
    FullAdder(a = a[6], b = b[6],   c = c5,  sum = out[6],  carry = c6);
    FullAdder(a = a[7], b = b[7],   c = c6,  sum = out[7],  carry = c7);

    FullAdder(a = a[8], b = b[8],   c = c7,  sum = out[8],  carry = c8);
    FullAdder(a = a[9], b = b[9],   c = c8,  sum = out[9],  carry = c9);
    FullAdder(a = a[10], b = b[10], c = c9,  sum = out[10], carry = c10);
    FullAdder(a = a[11], b = b[11], c = c10, sum = out[11], carry = c11);

    FullAdder(a = a[12], b = b[12], c = c11, sum = out[12], carry = c12);
    FullAdder(a = a[13], b = b[13], c = c12, sum = out[13], carry = c13);
    FullAdder(a = a[14], b = b[14], c = c13, sum = out[14], carry = c14);
    FullAdder(a = a[15], b = b[15], c = c14, sum = out[15], carry = c15);    // Omit the carry when do last bit add
}

这个加法器的一个问题是进位信号在16个门之间传递，效率比较低，有一种方法叫做carry look ahead，即超前进位加法器，优点是速度快，缺点是器件会增加很多：

图片名称

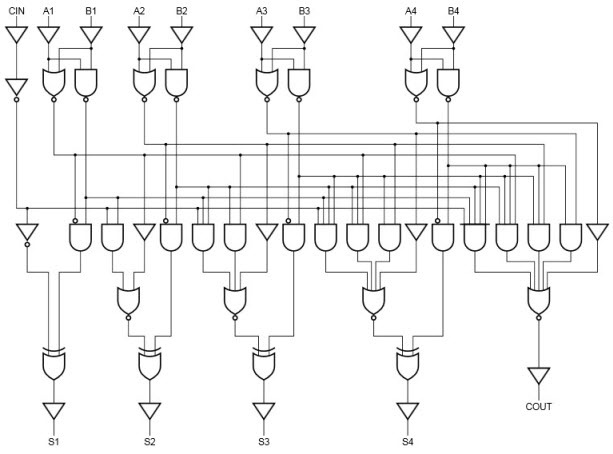
负数

如果我们用最高位表示符号，即可得到负数，$-x$可以使用如下公式进行计算：

例如对于二进制1001 (9)，对应的负数为$-(2^{4}-9) = (-7)$，我们称$9$为$-7$的补数，此处我们给出一个重要结论，两个负数相加可以表示为它们的补数相加：

由于我们抛弃了最高位，因此得到的补数和所需的负数结果相同。现在我们需要考虑给定一个数$x$，如何获取他的负数$-x$？这样我们就可以将减法转化为加法：$y-x=y+(-x)$。即我们需要如下芯片：

$\textrm{Input}: x$

$\textrm{Output}: -x$

这里我们运用一个小技巧：为了计算$(2^{n}-x)$，我们可以计算$2^n-x=1+(2^{n}-1)-x$，这样做的好处是$2^{n}-1$全部为1，做减法不需要借位，只需要将被减数按位翻转即可，所以这里我们得到了最终的结论，很重要，记住：一个负数等于其正数按位翻转后+1

算数逻辑单元（ALU）

现在我们来构造CPU中最重要的模块：ALU，其模块图如下所示：

图片名称

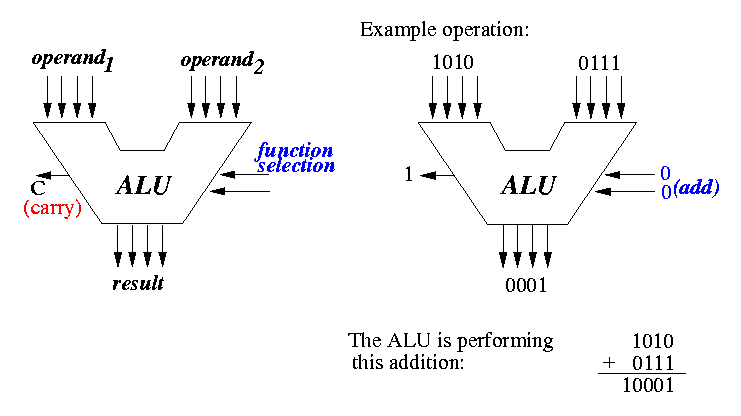
ALU：输入两个操作数和待执行的函数（算数或逻辑运算），给出指定结果，对于本课程的Hack ALU，其结构如下所示：

图片名称

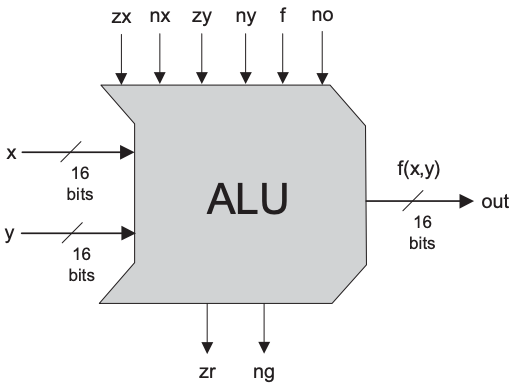
根据六个输入控制位zx, nx, zy, ny, f, no，可以选择不同的操作，Hack ALU支持的操作如下：

输出立即数 一元逻辑运算 二元逻辑运算 数学运算
0 x x & y -x
1 y x \ y -y
-1 !x x+1
!y y+1
x-1
y-1
x+y
x-y
y-x

同时，该ALU还有两个输出控制位zr, ng，表示输出是否为0或者为负数，ALU的HDL代码框架如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Chip name: ALU
Inputs: x[16], y[16], // Two 16-bit data inputs
    // Your ALU should first deal with zx, then nx
    zx, // Zero the x input
    nx, // Negate the x input
    zy, // Zero the y input
    ny, // Negate the y input
    f, // Function code: 1 for Add, 0 for And
    no // Negate the out output
Outputs: out[16], // 16-bit output
    zr, // True iff out=0
    ng // True iff out<0
Function: if zx then x = 0 // 16-bit zero constant
          if nx then x = !x // Bit-wise negation
          if zy then y = 0 // 16-bit zero constant
          if ny then y = !y // Bit-wise negation
          if f then out = x + y // Integer 2's complement addition
               else out = x & y // Bit-wise And
          if no then out = !out // Bit-wise negation
          if out=0 then zr = 1 else zr = 0 // 16-bit eq. comparison
          if out<0 then ng = 1 else ng = 0 // 16-bit neg. comparison
Comment: Overflow is neither detected nor handled

控制位的真值表如下：

图片名称

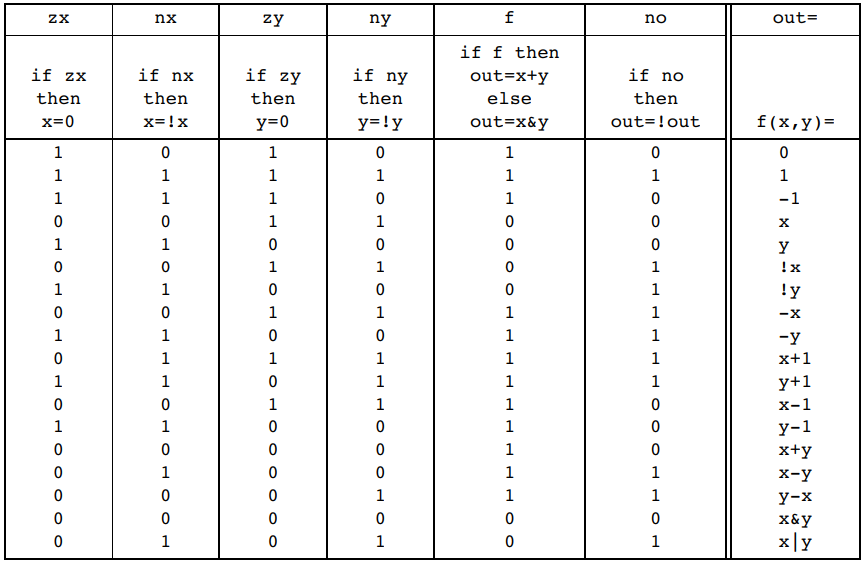
我们解释一下其中几行比较迷惑的

  • 计算1：为了计算1，我们可以对齐按位取反，得到b’1110，而b’1110为$-2$，即$-1+(-1)$，故只需要将$x$与$y$归零并按位取反即可
  • 计算$-x$：$-x=\overline x+1$，故$-x-1=\overline x$，两边同时取反，可得$\overline{-x-1}=x$，令$x=-x$，即可得到$\overline{x-1}=-x$。
  • 计算$x-y$：

参考文献

0%